Nesse post você vai entender o que é álgebra de Boole e como ela começou a ser estudada em meados do ano 1850. George Boole, um matemático, educador, filósofo e lógico trabalhou em diversas áreas das equações diferenciais e lógica. O seu livro mais famoso foi “As leis do pensamento” (1854) onde ele descreve a Álgebra de Boole.
Este livro foi de grande contribuição para as fundações da era da informática. O objeto de estudo de Boole eram os circuitos lógicos. Tais circuitos executam expressões que podem representar problemas do mundo real. Entretanto, a abstração de problemas do mundo real em circuitos é bastante complexa.
Portanto, Boole percebeu que alguns circuitos gerados por tabelas da verdade, entre outros dispositivos, admitem a simplificação. Assim, Boole propôs dispositivos que fossem capazes de simplificar circuitos para que o grau de dificuldade e custo na montagem fossem menor.
Em sua obra, Boole destaca a criação de postulados, ou seja, expressões que comprovadamente obterão sempre o mesmo resultado, estabelecendo então uma série de propriedades, equivalências. Para melhor compreender este assunto é interessante que já se tenha conhecimento prévio em funções e portas lógicas, aritmética binária e sistemas de numeração.
Conceitos básicos
No sistema binário só existem dois dígitos possíveis: o “0” e o “1”. Estes dígitos são as duas únicas constantes booleanas possíveis. Já uma variável booleana pode ser representada por qualquer letra, entretanto elas só podem assumir dois valores (0 ou 1).
Uma expressão booleana é uma expressão essencialmente matemática envolvendo constantes e/ou variáveis booleanas e seu resultado assume apenas dois valores (0 ou 1). Ex: S = A.B | S = A + B.C Na álgebra booleana há postulados (axiomas) a partir dos quais são estabelecidas várias propriedades.
Diversos destes postulados têm como objeto as propriedades da negação (complemento, inversor), adição (porta E) e soma (porta OU). Estes axiomas foram propostos e podem ser verificadas como equivalências lógicas. A demonstração da veracidade dos postulados pode ser feita utilizando as tabelas-verdade, constatando a equivalência
| Tipo | Postulado |
| Complemento | Se A = 0 então Ā = 1 Se A = 1 então Ā = 0 |
| Adição | 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 1 |
| Multiplicação | 0 . 0 = 0 0 . 1 = 0 1 . 0 = 0 1 . 1 = 1 |
| Notações alternativas | Ā = A’ Ā = ¬ A B.C = (B.C)’ |
Propriedades descritas na álgebra de Boole:
| Propriedade | Complemento | Adição | Multiplicação |
| Identidade | A” = A | A + 0 = A A + 1 = 1 A + A = A A + A’ = 1 | A . 0 = 0 A . 1 = A A . A = A A . A’ = 0 |
| Comutativa | A + (B + C) = (A + B) + C = A + B + C | A(B.C) = (A.B).C = A.B.C | |
| Distributiva | A + (B.C) = (A + B) . (A + C) | A.(B + C) = A.B + A.C |
Outras propriedades importantes
Absorção A + (A.B) = A A . (A+B) = A
Outras Identidades A + Ā.B = A + B (A+B).(A+C) = A + B.C
De Morgan (A . B)’ = A’ + B’ (A . B)’ = A’ + B’
Simplificando expressões booleanas
Usando a álgebra de boole é possível realizar a simplificação de expressões. Considerando que cada circuito corresponde a uma expressão, as simplificações de expressões correspondem a simplificações de circuitos. Há duas formas para simplificar expressões: fatoração e mapas de Veitch-Karnaugh.
A seguir serão abordadas as duas formas.
Simplificação por fatoração
A simplificação por fatoração é a que utiliza os postulados para realizar a simplificação das expressões. Ela tem uma estrutura semelhante a álgebra que é bastante trabalhada na matemática tradicional. Acompanhe no exemplo:
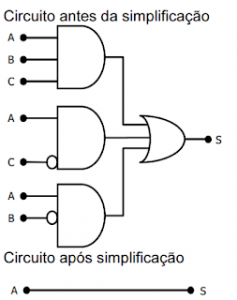
S = A.B.C + A.C’ + A.B’ = A.(B.C + C’ + B’)
distributiva = A.(B.C + (C’ + B’))
associativa = A.(B.C + ( (C’ + B’)’ )’)
identidade do complemento = A.(B.C + (C.B)’)
De Morgan = A.(B.C + (B.C)’ )
comutativa = A.(1)
identidade da adição (D+D’=1) = A identidade da multiplicação
Simplificação por mapas de Karnaught
A fatoração é um método eficiente, porém essencialmente algébrico e bastante vulnerável à falhas devido a interpretações incorretas. A realização da fatoração depende ainda da capacidade de memória dos postulados, ao qual não são poucos. O mapa de Karnaught é uma exposição visual de produtos fundamentais necessários para solução de uma soma de produtos. Confira o exemplo:
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| BC | A | 00 | 01 | 11 | 10 |
| 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
A simplificação utilizando mapas de Karnaught baseia-se no postulado que diz X + X’ = 1. Interpretando esta expressão, ela nos diz que em uma porta OU se tivermos 1 e 0 em cada entrada, a saída sempre será 1. Assim, esta entrada torna-se irrelevante.
Exemplo 1: S = ABC + ABC’ = AB (C + C’) = AB. Neste exemplo, aplicando o postulado podemos considerar a entrada C irrelevante (C + C’).
Exemplo 2:
| A | B | S |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| B A | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
- S = A
- S = AB’ + AB
A lógica do mapa é dispor os resultados da tabela verdade em uma matriz que obedece a quantidade de variáveis. No exemplo 2 observamos a existência das variáveis A e B, assim o mapa terá apenas estas duas variáveis nas linhas e colunas. A seguir são coletadas as variáveis que estão vizinhas (como foi destacado no mapa).
Após a identificação dos termos a serem analisados devemos identificar quais são as variáveis “fortes”, ou seja, aquelas que não se alteram. No mapa podemos perceber que a variável “A” é independente e não se altera, logo ela é uma variável forte, além disso, ela possui o valor 1, o que está de acordo com o seu estado então ela deverá ser incluída na expressão final em sua forma natural e não barrada. Já a variável “B” se alterna entre 0 e 1, assim ela é considerada uma variável fraca e deve ser eliminada da expressão final.
Os mapas podem ser utilizados com uma quantidade maior de variáveis, assim quanto maior o bloco selecionado para análise (vizinhos), maior o número de variáveis eliminadas e mais simplificada fica a expressão final:
- l Unidade: nenhuma variável eliminada;
- l Par: uma variável eliminada;
- l Quadra: duas variáveis eliminadas;
- l Oitava: três variáveis eliminadas;
A álgebra de boole é essencial para compreensão dos circuitos eletrônicos atuais.
Veja mais sobre isso na próxima aula.
Conclusão
Fica claro que a álgebra de boole é essencial dentro do contexto de eletrônica digital, além disso, a possibilidade de simplificar sistemas é uma necessidade latente. O consumo de recursos desnecessariamente é sempre um fator bastante prejudicial ao desenvolvimento de novas tecnologias. Cognitivamente a matemática pode ser um impeditivo na simplificação de expressão, por se tornar bastante densa em alguns casos. Os mapas de Karnaught podem auxiliar esta simplificação das expressões.