Nesse post vamos entender melhor como funciona a manipulação de imagens usando linguagens de programação e também vamos nos aprofundar em um fractal incrível chamado “fractal de koch”. Esse tutorial foi construído com dois objetivos principais: 1) mostrar que você mesmo pode criar software incríveis e animações usando apenas uma linguagem de programação. 2) mostrar que uma simples imagem e um padrão matemático pode ser um desafio bem legal de lógica.
Bom, antes de mais nada, preciso lembrar que você também pode aproveitar todo nosso conteúdo gratuitamente. Eu gosto bastante de criar aplicações práticas e também mostrar o contexto em que elas se aplicam. Então se você gosta de aplicações assim clique aqui e veja outros softwares similares.
Tratamento de imagens na computação
Como vamos trabalhar com imagens, primeiro precisamos entender que esse é um assunto “velho” dentro do mundo da ciência da computação. O nosso querido amigo Photoshop foi criado em 1988 por by Thomas and John Knoll e até hoje, anualmente, recebe atualizações e fica cada dia mais incrível. O software é realmente repleto de opções para artistas e tem suporte para inúmeras tarefas como tratamento de imagens, desenho e pintura digital, animações, etc.
O fato de ele ter sido criado a tanto tempo atrás mostra que o interesse da computação por novas soluções nesse contexto é bem grande. A indústria dos games, web design, UI/UX também tiveram uma grande contribuição e tornou a criação de imagens algo essencial para o cotidiano das pessoas.
No entanto, nosso foco aqui é a computação, e não conhecer mais sobre sistemas bem estabelecidos, certo?
Bom, vamos lá!
Ao criar os seus primeiros programas é comum ter exercícios que forçam você a desafiar sua lógica e testar seus limites. Frequentemente, os problemas são irrelevantes e sem contexto nenhum (o que não é um crime, dado o objetivo anteriormente citado). Geralmente encontramos problemas assim:
Crie um triângulo como esse usando apenas caracteres:
* ** *** **** ***** ******
Certo, isso é realmente um desafio para treinar sua lógica e também como melhor utilizar laços de repetição. Mas vamos combinar, isso não pode nem mesmo ser considerado uma imagem, na verdade, é uma abstração de um triângulo.
Essa visualização pobre é resultado de uma limitação comum a várias linguagens de programação que é a exibição da saída de dados no terminal. Esse recurso que já foi considerado o “supra sumo” das interfaces, hoje é só chato mesmo.
Antigamente, existia ainda um tipo de arte (derivada dessas limitações) chamada de “text art” ou “arte com texto”. As pessoas (artistas) se dedicavam a criar figuras bastante elaboradas usando apenas texto. Se você assiste algumas lives na Twitch já deve ter visto algumas figuras subindo no chat do streamer feitas apenas com texto. Quer ver alguns exemplos? clique aqui.
Formatos de imagem
Ao vasculhar a internet por ai, você encontra muitos formatos de imagens, sendo que os mais famosos são o JPG e também o PNG. Cada formato de imagem possui um “super poder”, por exemplo, o JPG foi feito para ser altamente compactado, ou seja, imagens em JPG tendem a ser muito menores do que as imagens em PNG. Já no caso do PNG, é possível criar imagens que são “transparentes”, para isso o arquivo carrega em suas informações um dado adicional que permite os sistemas operacionais e softwares de manipulação tratar determinados pixels como transparentes.
No entanto, existem alguns formatos de imagens que são bastante exóticos, esse é o caso do PGM. O formato PGM é excelente para ilustrar como podemos criar imagens usando programação. PGM é uma sigla para “Portable Gray Map”, como o próprio nome já diz ele representa imagens usando um mapa de pixels apenas em escala de cinza. Esse formato foi definido como parte de um projeto maior chamado Netpbm criado pelo desenvolvedor Jef Poskanzer’s. Esse pacote gráfico possui vários formatos descritos, inclusive o PGM e o PPM (versão alternativa que inclui cores RGB).
A especificação desse formato é bastante clara e simples, existem 3 informações essenciais de “cabeçalho”, são elas: Número Mágico, dimensões, pontos de cinza.
Então ao escrever um arquivo PGM ele deve começar assim:
P2 #Representa o número mágico
24 7 # dimensões 24 pixels por 7
15 # 15 pontos de cinzaPor fim, devemos colocar cada pixel da imagem em formato de matriz e separado por um espaço. Um exemplo dado pela própria documentação oficial é esse:
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 3 3 3 3 0 0 7 7 7 7 0 0 11 11 11 11 0 0 15 15 15 15 0
0 3 0 0 0 0 0 7 0 0 0 0 0 11 0 0 0 0 0 15 0 0 15 0
0 3 3 3 0 0 0 7 7 7 0 0 0 11 11 11 0 0 0 15 15 15 15 0
0 3 0 0 0 0 0 7 0 0 0 0 0 11 0 0 0 0 0 15 0 0 0 0
0 3 0 0 0 0 0 7 7 7 7 0 0 11 11 11 11 0 0 15 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0Essa imagem ao ser aberta em um editor de imagens é mostrada assim:
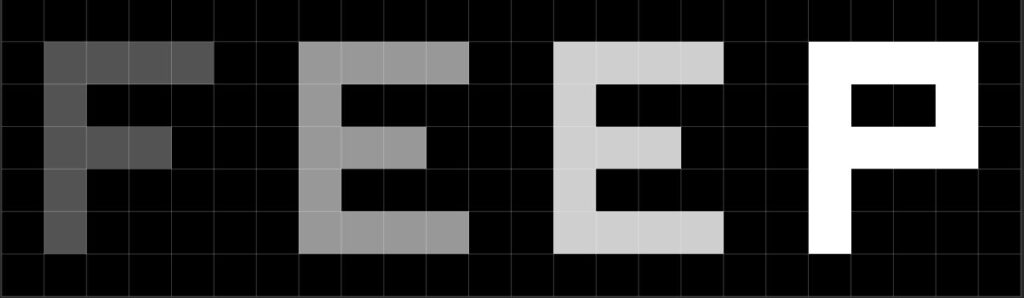
Esse exemplo mostra claramente como é possível que imagens possam ser reduzidas simplesmente a mapas de pixels. Sendo assim, criar e manipular imagens depende apenas do seu conhecimento para manipular matrizes!
Como mostrar imagens PGM usando Python
Ao usar o Python, é possível criar matrizes para representar nossas imagens. Então, podemos criar um mini-software apenas para fazer a leitura e mostrar essas imagens.
import re
import numpy as np
from matplotlib import pyplot as plt
## mostra de um arquivo
def mostrarImagemDoArquivo(nomeDoArquivo):
with open(nomeDoArquivo + '.pgm') as f:
s = f.read()
l=re.findall(r'[0-9P]+',s)
w, h = int(l[1]), int(l[2])
ni = np.array(l[4:],dtype=np.uint8).reshape((h,w))
from matplotlib import pyplot as plt
plt.imshow(ni, cmap='gray')
plt.show()Lembre-se que ao ler os arquivos devemos usar as informações de cabeçalho (numero mágico, tamanho e pontos de cinza). No entanto, a parte triste é que o Jupyter notebook não tem suporte para o formato pgm, então tenho que fazer uma bela gambiarra e usar uma função para converter os arquivos que desejo mostrar aqui pra vocês.
A função para mostrar as imagens ficou assim:
## mostra sem salvar em um arquivo
def mostrarImagem(mapa, save = False, path = "", animation = False, index = 0, direction = ""):
ni = np.array(mapa)
plt.imshow(ni, cmap='gray')
if save == False:
plt.show()
if save == True and animation == False:
plt.savefig(pathToSave.format("output.png"))
if save == True and animation == True:
plt.savefig(pathToSave.format(str(index) + "Fig" + direction + ".png"))Veja que essa função possui vários parâmetros, eles são opcionais e são usados para armazenar figuras e criar pequenas animações. Além disso, perceba também que o “mapa” recebido nessa imagem é apenas uma matriz em que cada pixel representa um ponto de cinza.
Primeiros passos para criar imagens
Se você quer criar uma imagem totalmente preta com aspectos específicos (ex. 50 x 40), precisamos definir uma matriz assim. Então podemos usar um código bem simples:
# cria um vetor
mp = [0,0,0,0,0,0,0,0,0,0,0,0]
mapa = []
# adiciona varias vezes o vetor criado a matriz
mapa.append(mp)
mapa.append(mp)
mapa.append(mp)
mapa.append(mp)
mapa.append(mp)
mapa.append(mp)
mapa.append(mp)
# mostra a imagem
mostrarImagem(mapa)O resultado disso é bastante simples. Uma imagem totalmente preta:
Ah mas se quisermos criar apenas algumas listras nessa imagem variando o tom do cinza? Veja o seguinte código:
mp = [10,10,10,10,10,10,10,10,10,10,10,10]
mp2 = [0,0,0,0,0,0,0,0,0,0,0,0]
mp3 = [5,5,5,5,5,5,5,5,5,5,5,5]
mapa = []
mapa.append(mp)
mapa.append(mp2)
mapa.append(mp3)
mapa.append(mp2)
mapa.append(mp)
mapa.append(mp3)
mapa.append(mp2)
mostrarImagem(mapa)O resultado fica assim:

Então agora podemos criar uma imagem, vamos criar uma função para encapsular esse comportamento:
def criarImagem(altura, largura, pontosDeCinza):
vetLargura = []
for x in range(largura):
vetLargura.append(0)
img = []
for y in range(altura):
img.append(vetLargura)
return img
## testa criando uma imagem 50x50
imagem = criarImagem(20,20,15)
mostrarImagem(imagem)Essa função recebe por parâmetro a quantidade de pontos na altura e largura e adiciona e retorna uma imagem preta com aqueles pontos.
Certo, mas agora eu gostaria de escrever um único pontinho dentro da minha imagem… para isso vou fazer o seguinte:
import numpy as np
def escrevePonto(imagem,x,y,pontosDeCinza):
img = np.array(imagem)
img[y,x] = pontosDeCinza
return img
imagem = escrevePonto(imagem,6,5,15)
mostrarImagem(imagem)Agora nos podemos criar até mesmo algumas animações fazendo nosso pontinho se mover:
Ah, você quer saber como eu fiz isso? é bem simples, eu só criei imagens para cada alteração da nossa imagem, então fui nesse site, fiz upload da imagem e criei um GIF.
Agora, se nós quisermos criar uma linha, precisamos fazer uma simples alteração:
imagem = criarImagem(20,20,15)
for i in range(2,15):
imagem = escrevePonto(imagem,i,2,15)
mostrarImagem(imagem, save=True, path = pathToSave, animation = True, index = i)
#mostrarImagem(imagem)Perceba que nesse trecho eu apenas removi a criação da imagem a cada iteração do for, assim a linha se preserva. O resultado é o seguinte:
Agora vamos tentar algo mais “elaborado”, vamos tentar criar uma simples curva de 90º para a direita (ou para baixo, tanto faz). Para isso vamos precisar alterar hora a posição X e hora a posição Y, assim temos uma curva com ângulo reto. Veja o código:
## define um ponto de partida
x,y = 5,5
## cria um mini vetor para armazenar onde o ponto "parou"
ponteiro = [x,y]
# cria a imagem
imagem = criarImagem(20,20,15)
index = 0
## faz uma reta da esquerda para direita (incrementando o eixo x)
for vx in range(x,15):
imagem = escrevePonto(imagem,vx,y,15)
index += 1
ponteiro[0] = vx
mostrarImagem(imagem, save=True, path = pathToSave, animation = True, index = index, direction ="l")
#mostrarImagem(imagem)
## Faz uma reta para baixo incrementando o eixo Y
for vy in range(y,15):
imagem = escrevePonto(imagem,ponteiro[0],vy,15)
index += 1
mostrarImagem(imagem, save=True, path = pathToSave, animation = True, index = index, direction ="l")
#mostrarImagem(imagem)Veja o resultado:

Podemos repetir essa operação até chegarmos em uma figura fechada, como um quadrado por exemplo:

Certo, até funciona, mas não me parece muito intuitivo… na verdade eu gostaria de definir um ponto inicial e informar a quantidade de pontos que quero avançar. Além disso, gostaria de avançar em direções diferentes (cima, baixo, esquerda direita).
Então vamos uma função que recebe como parâmetro a ação desejada:
def avancar(imagem, direcao, pontoDePartida, pontosParaAvancar, corDoPonto = 15, salvar = False, path = "", index = 0):
x,y = pontoDePartida
if direcao == ">":
for m in range(x, x + pontosParaAvancar):
imagem = escrevePonto(imagem,m,y,corDoPonto)
index += 1
if salvar == True:
mostrarImagem(imagem, save=True, path = pathToSave, animation = True, index = index, direction = "d")
else:
mostrarImagem(imagem)
return {"imagem": imagem, "ponteiro": [x + pontosParaAvancar, y], "index": index}
if direcao == "v":
for m in range(y, y + pontosParaAvancar):
imagem = escrevePonto(imagem,x,m,corDoPonto)
index += 1
if salvar == True:
mostrarImagem(imagem, save=True, path = pathToSave, animation = True, index = index, direction = "b")
else:
mostrarImagem(imagem)
return {"imagem": imagem, "ponteiro": [x , y + pontosParaAvancar], "index": index}
if direcao == "^":
for m in range(y, y - pontosParaAvancar, -1):
imagem = escrevePonto(imagem,x,m,corDoPonto)
index += 1
if salvar == True:
mostrarImagem(imagem, save=True, path = pathToSave, animation = True, index = index, direction = "c")
else:
mostrarImagem(imagem)
return {"imagem": imagem, "ponteiro": [x , y - pontosParaAvancar], "index": index}
if direcao == "<":
for m in range(x, x - pontosParaAvancar, -1):
imagem = escrevePonto(imagem,m,y,corDoPonto)
index += 1
if salvar == True:
mostrarImagem(imagem, save=True, path = pathToSave, animation = True, index = index, direction = "e")
else:
mostrarImagem(imagem)
return {"imagem": imagem, "ponteiro": [x - pontosParaAvancar , y ], "index": index}
Agora podemos apenas chamar a função “avançar” passando os parâmetros necessários:
pathToSave = r"output\animacao4\{}"
# cria a imagem
imagem = criarImagem(20,20,15)
r1 = avancar(imagem,">", [5,5], 10, 15, salvar = True, path = pathToSave )
r2 = avancar(r1["imagem"],"v", r1["ponteiro"], 10, 15, salvar = True, path = pathToSave, index = r1["index"])
r3 = avancar(r2["imagem"],"<", r2["ponteiro"], 10, 15, salvar = True, path = pathToSave, index = r2["index"])
r4 = avancar(r3["imagem"],"^", r3["ponteiro"], 10, 15, salvar = True, path = pathToSave, index = r3["index"])
Temos agora o mesmo resultado, porém, abstraído em uma única função. Mas daí vem a pergunta, e se eu quiser me movimentar na diagonal? Podemos configurar também essa função para isso:
def avancar(imagem, direcao, pontoDePartida, pontosParaAvancar, corDoPonto = 15, salvar = False, path = "", index = 0):
x,y = pontoDePartida
if direcao == ">":
for m in range(x, x + pontosParaAvancar):
imagem = escrevePonto(imagem,m,y,corDoPonto)
index += 1
if salvar == True:
mostrarImagem(imagem, save=True, path = pathToSave, animation = True, index = index, direction = "d")
else:
mostrarImagem(imagem)
return {"imagem": imagem, "ponteiro": [x + pontosParaAvancar, y], "index": index}
if direcao == "v":
for m in range(y, y + pontosParaAvancar):
imagem = escrevePonto(imagem,x,m,corDoPonto)
index += 1
if salvar == True:
mostrarImagem(imagem, save=True, path = pathToSave, animation = True, index = index, direction = "b")
else:
mostrarImagem(imagem)
return {"imagem": imagem, "ponteiro": [x , y + pontosParaAvancar], "index": index}
if direcao == "^":
for m in range(y, y - pontosParaAvancar, -1):
imagem = escrevePonto(imagem,x,m,corDoPonto)
index += 1
if salvar == True:
mostrarImagem(imagem, save=True, path = pathToSave, animation = True, index = index, direction = "c")
else:
mostrarImagem(imagem)
return {"imagem": imagem, "ponteiro": [x , y - pontosParaAvancar], "index": index}
if direcao == "<":
for m in range(x, x - pontosParaAvancar, -1):
imagem = escrevePonto(imagem,m,y,corDoPonto)
index += 1
if salvar == True:
mostrarImagem(imagem, save=True, path = pathToSave, animation = True, index = index, direction = "e")
else:
mostrarImagem(imagem)
return {"imagem": imagem, "ponteiro": [x - pontosParaAvancar , y ], "index": index}
if direcao == "db":
my = y
for m in range(x, x + pontosParaAvancar):
imagem = escrevePonto(imagem,m,my,corDoPonto)
index += 1
my += 1
if salvar == True:
mostrarImagem(imagem, save=True, path = pathToSave, animation = True, index = index, direction = "db")
else:
mostrarImagem(imagem)
return {"imagem": imagem, "ponteiro": [x + pontosParaAvancar , my], "index": index}
if direcao == "dc":
my = y
for m in range(x, x + pontosParaAvancar):
imagem = escrevePonto(imagem,m,my,corDoPonto)
index += 1
my -= 1
if salvar == True:
mostrarImagem(imagem, save=True, path = pathToSave, animation = True, index = index, direction = "dc")
else:
mostrarImagem(imagem)
return {"imagem": imagem, "ponteiro": [x + pontosParaAvancar , my], "index": index}
if direcao == "eb":
my = y
for m in range(x, x - pontosParaAvancar, -1):
imagem = escrevePonto(imagem,m,my,corDoPonto)
index += 1
my += 1
if salvar == True:
mostrarImagem(imagem, save=True, path = pathToSave, animation = True, index = index, direction = "eb")
else:
mostrarImagem(imagem)
return {"imagem": imagem, "ponteiro": [x - pontosParaAvancar , my], "index": index}
if direcao == "ec":
my = y
for m in range(x, x - pontosParaAvancar, -1):
imagem = escrevePonto(imagem,m,my,corDoPonto)
index += 1
my -= 1
if salvar == True:
mostrarImagem(imagem, save=True, path = pathToSave, animation = True, index = index, direction = "ec")
else:
mostrarImagem(imagem)
return {"imagem": imagem, "ponteiro": [x - pontosParaAvancar , my], "index": index}Ao fazer essa configuração, podemos criar algo como um losango, para isso codificamos assim:
pathToSave = r"output\animacao5\{}"
# cria a imagem
imagem2 = criarImagem(21,21,15)
r1 = avancar(imagem2,"dc", [0,10], 10, 15, salvar = True, path = pathToSave, index = 0)
r2 = avancar(r1["imagem"],"db", r1["ponteiro"], 10, 15, salvar = True, path = pathToSave, index = r1["index"])
r3 = avancar(r2["imagem"],"eb", r2["ponteiro"], 10, 15, salvar = True, path = pathToSave, index = r2["index"])
r4 = avancar(r3["imagem"],"ec", r3["ponteiro"], 10, 15, salvar = True, path = pathToSave, index = r3["index"])
O resultado fica mais ou menos assim:
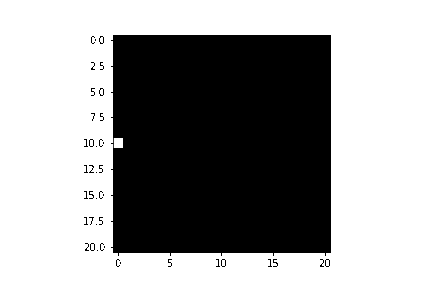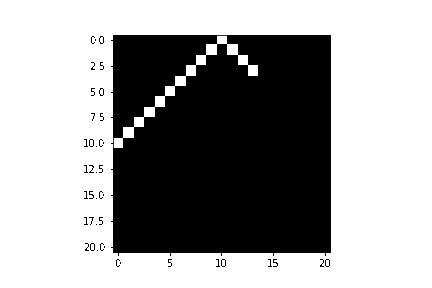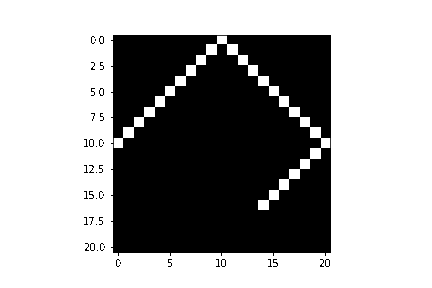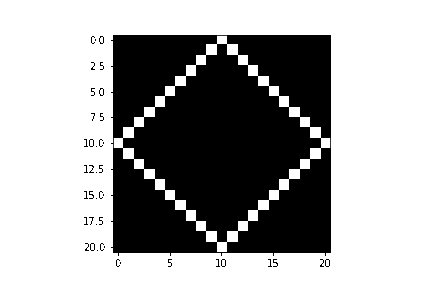
Por fim, temos algo como parecido com uma biblioteca de controle gráfico, no entanto, precisamos ressaltar o quanto essa biblioteca é limitada. Primeiramente, ela não permite fazer facilmente uma figura com angulações diferentes de 45 graus e além disso, são necessários muitos parâmetros para um uso básico.
A biblioteca turtle
Existem algumas bibliotecas gráficas que já são “built-in” do python, o principal exemplo é a biblioteca “turtle”. Ela é baseada no plano cartesiano e você pode posicionar a sua “caneta” na tela e mover para qualquer direção (frente e atrás).
# para importar nossa "tartaruga" fazemos:
import turtle
# mover a tartaruga para frente:
turtle.forward(100)
# finalizar o processamento
turtle.done()O resultado fica assim:
A parte que torna essa biblioteca muito melhor que nossa implementação é a capacidade de rotacionar sua “tartaruga” e se movimentar em outra direção.
# para importar nossa "tartaruga" fazemos:
import turtle
# mover a tartaruga para frente:
turtle.forward(100)
## 90 representa a angulação de giro
turtle.right(90)
turtle.forward(100)
turtle.right(90)
turtle.forward(100)
turtle.right(90)
turtle.forward(100)
turtle.right(90)
# finalizar o processamento
turtle.done()O resultado desse código é um simples quadradinho:
O fractal de Koch
Agora vamos adentrar em um assunto bem legal: os fractais. Esse tipo de figura possui uma definição um pouco estranha:
Um fractal é um subconjunto do espaço euclidiano com uma dimensão fractal que excede estritamente sua dimensão topológica. Geralmente exibem padrões semelhantes em escalas cada vez menores, uma propriedade chamada auto-similaridade , também conhecida como expansão de simetria ou desdobramento de simetria; se essa replicação for exatamente a mesma em todas as escalas.
Fonte: wikipedia
Mas, resumindo, um fractal é uma figura formada essencialmente por um padrão matemático. Em geral esse padrão é repetitivo e isso acontece infinitamente, tornando a figura bastante interessante. Um exemplo é o conjunto de mendelbrot:

O mais interessante é que essas figuras ocorrem na natureza e são muito legais né?
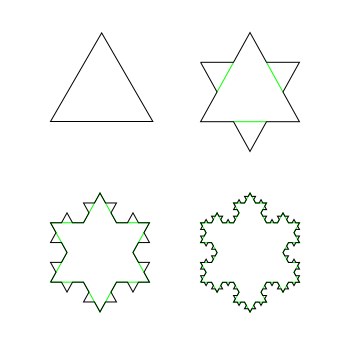
Um desses fractais foi descoberto por um matemático suéco chamado Helge von Koch, por isso, o nome do fractal é “fractal de koch”, porém, eu costumo chamar de fractal do floco de neve mesmo. Na minha opinião esse fractal é incrível pela sua simplicidade e ao mesmo tempo também pela sua complexidade matemática.
O fractal é basicamente um triangulo que vai se segmentando em três partes. Isso acontece tantas vezes que seu formato fica muito parecido com um floco de neve.
Se quisermos desenhar a primeira iteração desse fractal podemos escrever com o turtle uma versão:
# para importar nossa "tartaruga" fazemos:
import turtle
# Essa é a iteração 1 do nosso algoritmo de koch
turtle.forward(50)
turtle.left(60)
turtle.forward(50)
turtle.right(120)
turtle.forward(50)
turtle.left(60)
turtle.forward(50)
# finalizar o processamento
turtle.done()O resultado fica mais ou menos assim:
O grande problema, é como podemos avançar para o próximo nível (próxima iteração). Teóricamente, cada segmento que desenhamos (retas) precisa ser dividida em 3 partes iguais e na parte central é desenhado a pontinha do novo triângulo. Mas, fazer isso se repetir infinitas vezes pode ser um pouco dificil usando apenas iterações comuns, por esse motivo o fractal de koch usa recursão!
Nesse caso a recursão é perfeita visto que permite que nós façamos os desenhos dos segmentos de reta de acordo com o tamanho inicial definido e também na profundidade desse fractal. Para isso vamos começar nosso código simplesmente instanciando nossa tartaruga e o tamanho inicial do nosso floco de neve.
import turtle
import math
wn = turtle.Screen()
tamanhoDoFloco = 200
O tamanho do nosso floco é importante porque esse valor será dividido várias vezes para representar a quantidade de pixels que terá cada segmento. A seguir vamos fazer algumas configurações básicas da nossa tartaruga:
# Configura a tartaruga
t = turtle.Turtle()
t.speed(50*(depth+1))
t.penup()
t.setposition((10,10))
t.pendown()
t.left(60)Por fim, vamos definir a função que será recursiva e realmente desenhará nosso fractal:
import turtle
import math
wn = turtle.Screen()
tamanhoDoFloco = 200
# Profundidade escolhida
profundidade = 1
# Set up the turtle
t = turtle.Turtle()
t.speed(50*(profundidade+1))
t.penup()
t.setposition((10,10))
t.pendown()
t.left(60)
def desenhar_segmento(t, corrida, minhaProfundidade, profundidade):
if minhaProfundidade == profundidade:
# desenha o segmento quando a sua profundidade chega no limite definido (aqui é o pé da recursão)
t.fd(corrida)
else:
minhaCorrida = corrida/3.0
# Make each straight bit into a smaller version of ourselves
desenhar_segmento(t, minhaCorrida, minhaProfundidade+1, profundidade)
t.left(60)
desenhar_segmento(t, minhaCorrida, minhaProfundidade+1, profundidade)
t.right(120)
desenhar_segmento(t, minhaCorrida, minhaProfundidade+1, profundidade)
t.left(60)
desenhar_segmento(t, minhaCorrida, minhaProfundidade+1, profundidade)
# Draw the basic triangle outline
for ii in range(3):
desenhar_segmento(t, tamanhoDoFloco, 0, profundidade)
t.right(120)
wn.exitonclick()
turtle.done()Nosso resultado final é esse:
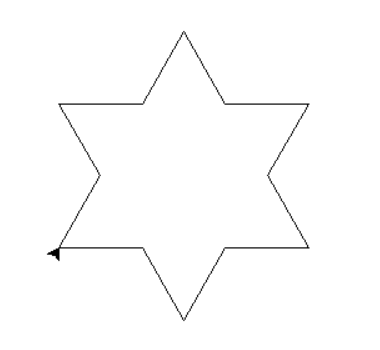
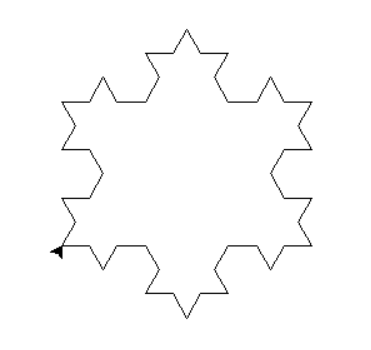
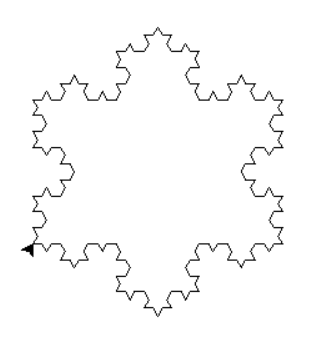
Quer acessar o código completo?