Nessa aula iremos continuar modelando nosso conhecimento a cerca da regressão linear, porém, nesse momento, exploraremos uma outra possibilidade que é a regressão linear múltipla. Essa técnica se assemelha muito à regressão linear simples, mas nesse método utilizamos mais de uma variável para predizer o valor resultado.
Relembrando: o que é regressão linear?
A regressão linear é uma abordagem linear para modelar a relação entre uma resposta escalar e uma ou mais variáveis explicativas (também conhecidas como variáveis dependentes e independentes).
Meu deus, já ficou complicado… mas calma, não é.
Vamos para um exemplo bem simples, imagine o seguinte gráfico:
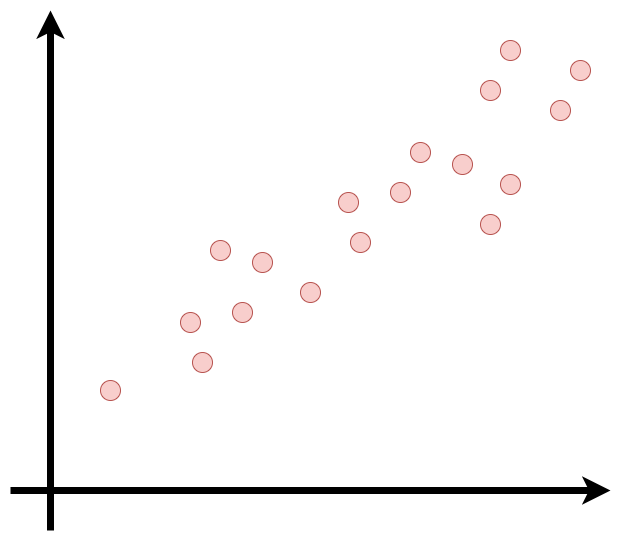
Você consegue perceber que existe uma tendência de crescimento linear entre os pontos que estão em vermelho. Quando o eixo X se desloca positivamente o eixo Y também possui uma resposta similar. Assim nós podemos traçar uma reta que descreve esse movimento e “prever” onde os próximos pontos estarão.
Essa reta obedece as regras que você ja deve ter visto na matemática de funções do primeiro grau (Ax + B).
O que é regressão linear múltipla
Até agora falamos de regressão linear, porém ela pode assumir dois tipos: simples e múltipla. Quando uma variável apenas é gerada (apenas um ponto) chamamos de regressão linear simples, porém quando temos para mais de um, o processo é chamado de regressão linear múltipla .
Muitas vezes uma única variável preditora não será capaz de explicar tudo a respeito da variável resposta. Por exemplo, a renda de uma determinada pessoa (variável resposta) é influenciada por diversas variáveis, tais como sexo, idade, escolaridade entre outras. Assim, precisamos realizar uma regressão linear múltipla.
Quando o número de preditores (variáveis independentes) é grande, é necessário utilizar técnicas para remover preditores que não estejam associados às respostas, ajustando o modelo de regressão. Ou seja, se temos um modelo descrito por duas variáveis e uma delas não “ajuda” muito na predição, é melhor removê-lo.
Como aplicar a regressão linear múltipla
Vamos tentar criar um cenário mais real para conseguirmos compreender essa tal regressão linear múltipla. Imagine que você tem um dataset com informações sobre carros:
| Car | Model | Volume | Weight | CO2 | |
| 0 | Toyota | Aygo | 1000 | 790 | 99 |
|---|---|---|---|---|---|
| 1 | Mitsubishi | Space Star | 1200 | 1160 | 95 |
| 2 | Skoda | Citigo | 1000 | 929 | 95 |
| 3 | Fiat | 500 | 900 | 865 | 90 |
| 4 | Mini | Cooper | 1500 | 1140 | 105 |
| 5 | VW | Up! | 1000 | 929 | 105 |
| 6 | Skoda | Fabia | 1400 | 1109 | 90 |
| 7 | Mercedes | A-Class | 1500 | 1365 | 92 |
| 8 | Ford | Fiesta | 1500 | 1112 | 98 |
| 9 | Audi | A1 | 1600 | 1150 | 99 |
| 10 | Hyundai | I20 | 1100 | 980 | 99 |
| 11 | Suzuki | Swift | 1300 | 990 | 101 |
| 12 | Ford | Fiesta | 1000 | 1112 | 99 |
| 13 | Honda | Civic | 1600 | 1252 | 94 |
| 14 | Hundai | I30 | 1600 | 1326 | 97 |
| 15 | Opel | Astra | 1600 | 1330 | 97 |
| 16 | BMW | 1 | 1600 | 1365 | 99 |
| 17 | Mazda | 3 | 2200 | 1280 | 104 |
| 18 | Skoda | Rapid | 1600 | 1119 | 104 |
| 19 | Ford | Focus | 2000 | 1328 | 105 |
| 20 | Ford | Mondeo | 1600 | 1584 | 94 |
| 21 | Opel | Insignia | 2000 | 1428 | 99 |
| 22 | Mercedes | C-Class | 2100 | 1365 | 99 |
| 23 | Skoda | Octavia | 1600 | 1415 | 99 |
| 24 | Volvo | S60 | 2000 | 1415 | 99 |
| 25 | Mercedes | CLA | 1500 | 1465 | 102 |
| 26 | Audi | A4 | 2000 | 1490 | 104 |
| 27 | Audi | A6 | 2000 | 1725 | 114 |
| 28 | Volvo | V70 | 1600 | 1523 | 109 |
| 29 | BMW | 5 | 2000 | 1705 | 114 |
| 30 | Mercedes | E-Class | 2100 | 1605 | 115 |
| 31 | Volvo | XC70 | 2000 | 1746 | 117 |
| 32 | Ford | B-Max | 1600 | 1235 | 104 |
| 33 | BMW | 2 | 1600 | 1390 | 108 |
| 34 | Opel | Zafira | 1600 | 1405 | 109 |
| 35 | Mercedes | SLK | 2500 | 1395 | 120 |
Podemos importar esse dataset usando um arquivo CSV usando o pandas:
import pandas from sklearn import linear_model df = pandas.read_csv("carros.csv")
Depois você pode simplesmente “pegar” colunas de um dataset para usá-las como fonte de informação para treinar um regressor:
X = df[['Weight', 'Volume']] y = df['CO2'] regr = linear_model.LinearRegression() regr.fit(X, y) # testando o regressor predictedCO2 = regr.predict([[2300, 1300]]) print(predictedCO2)
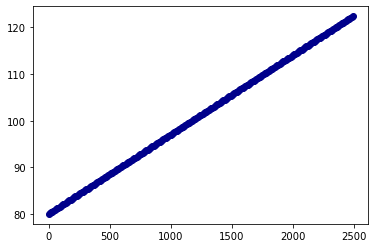
Mas antes de mais nada, vamos fazer algumas análises… Quando criamos um scatter plot usando volume e peso, temos o seguinte resultado:
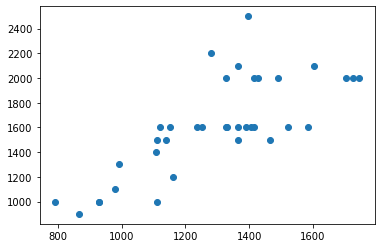
import matplotlib.pyplot as plt import numpy as np a = df['Weight'] b = df['Volume'] plt.scatter(a,b)
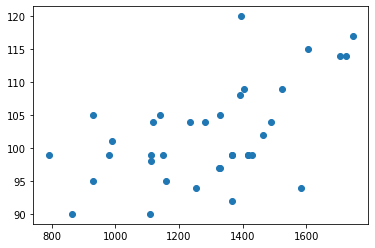
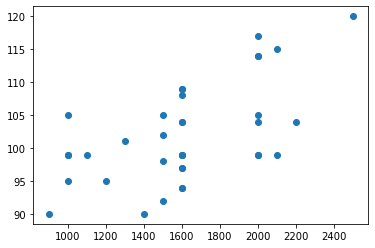
Mas, ao criar esse mesmo gráfico usando outras dimensões como o CO2 o gráfico se torna um pouco menos “linear”:

Weight X CO2 
Volume X CO2
É impossível representar um scatter plot com 3 dimensões (2 no eixo X e 1 no Y), porém, observe que no código que treinamos nosso regressor nós fizemos exatamente isso:
# observe aqui o eixo X com 2 dimensões X = df[['Weight', 'Volume']] y = df['CO2'] regr = linear_model.LinearRegression() regr.fit(X, y)
Portanto, ao criar uma regressão linear com 2 conjuntos de valores para apenas 1 eixo estamos criando uma regressão linear múltipla. Esse regressor obedece uma função do primeiro grau que é representada pela reta abaixo: