Nesse post você via entender como funcionam três algoritmos importantes: Principal Analysis (PCA), Singular Value Decomposition (SVD) e Latent Semantic Analysis (LSA). Porém, antes disso é preciso relembrar alguns conceitos importatantes apresentados anteriormente na nossa série de posts sobre PLN.
Assim como foi explicado anteriormente, um dos maiores desafios da área de PLN é a falta de estrutura em textos escritos em linguagem natural. Uma das tentativas de criar uma base de dados passível de ser manipulada é a redução de um texto a um vetor de frequência de palavras.
Veja um exemplo:
Sentença: Minha casa é amarela e fica entre uma casa vermelha e outra verde.
Vetor de palavras: [[Casa – Fr: 2], [minha – Fr:1]] …
* Fr: frequência
Entenda melhor sobre isso: O que são vetores de palavras
Utilizando esses vetores de palavras podemos avaliar quais delas são mais importantes para o texto com base em sua frequência. Essa informação é muito importante para construção de várias aplicações, como por exemplo, detectores detectores de SPAM ou análise de sentimentos. Porém, essa abordagem possui alguns problemas e um deles é a grande quantidade de sinônimos e polissemia em textos de linguagem natural. Na língua inglesa encontramos palavras como:
“buy” e “purchase”
“big” e “large”
“quick” e “Speedy”
Exemplo de polissemia:
“man” – pode ser utilizado para se referir ao oposto de um animal, ou oposto a fêmea do homem (mulher), ou apenas com sentido casual “hey, man!”.
“milk” – pode se referir ao liquido gerado por mamíferos ” the cat is producing milk for its babies” ou também pode se referir a tirar vantagem de uma condição ou situação. “I’m going to milk it for all it’s worth”.
Sendo assim, para resolver este problema muitas vezes preciso combinar palavras com um significado semelhante. Assim, você poderá ver as palavras Desktop e PC juntas, pois seu significado estão altamente relacionados.
Tá, mas onde entra o Latent Semantic Analysis nisso?
O trabalho do algoritmo de Latent Semantic Analisys (LSA) é encontrar variáveis que possam representar um conjunto de palavras com o mesmo significado. Assim, seria possível que a dimensionalidade dos dados analisados seja bem menor que o original, possibilitando um processamento mais rápido dos dados.
É importante notar que o LSA ajuda a resolver o problema dos sinônimos combinando variáveis correlatas, porém existe ainda o problema da polissemia no qual este algoritmo não trata.
Certo, mas e o Principal Component Analysis (PCA) e Singular Value Decomposition (SVD)?
Vamos olhar primeiro para o PCA, entender o que este algoritmo faz de uma forma geral. O PCA nada mais é do que uma versão mais simples do SVD e seu objetivo é transformar todos vetores de entrada.
Esse procedimento matemático utiliza uma transformação ortogonal (ortogonalização de vetores) para converter um conjunto de observações de variáveis possivelmente correlacionadas num conjunto de valores de variáveis linearmente não correlacionadas chamadas de componentes principais. Essa parte é um pouco complicada, mas não vou entrar em detalhes matemáticos aqui.
O objetivo de aplicar esse algoritmo é reduzir os vetores de palavras aos componentes principais. Entenda que reduzindo as informações, nem sempre você estará reduzindo a habilidade de predição (por isso ele é importante). Ao realizar o Processamento de Linguagem Natural o vocabulário é bastante grande, e os ruídos são bastante comuns, então ao retirar o ruído é possível realizar melhor a generalização e uma forma nova de olhar os novos dados e o PCA ajuda a realizar a remoção de ruídos.
Agora que compreendemos que o PCA localiza correlações entre os inputs. Estamos preparados para compreender (superficialmente) o funcionamento do SVD. O Singular Value Decomposition apenas realiza dois PCAs ao mesmo tempo e é um método de decomposição de matriz para reduzir uma matriz às suas partes constituintes, a fim de tornar mais simples alguns cálculos de matriz subsequentes.
Mãos no código
Usando LSA
Calma, felizmente você não precisa entender toda a teoria por trás do LSA, SVD e PCA para utilizá-los em seus projetos. Para este exemplo iremos utilizar um Dataset chamado book titles.
# primeiro você precisa importar as bibliotecas nltk, numpy e matplotlib (lembre-se de instalar elas em seu ambiente)
import nltk
import numpy as np
import matplotlib.pyplot as plt
# você também precisa importar um stemmer e um lematizador que já existe dentro do NLTK
import from nltk.stem import WordNetLemmatizer
# importe também o algoritmo de SVD presente no SKLearn (também é preciso instalar esse pacote)
from sklearn.decomposition import Truncated SVD
#crie uma nova instância do objeto wordnetLemmatizer.
wordnet_lemmatizer = WordnetLemmatizer()
# faça a leitura do dataset (lembre-se de colocá-lo em uma pasta que o python consiga encontrá-lo)
titles = [ line.rstrip() for line in open ('all_book_titles.txt')]
Tudo isso é bastante similar ao que realizamos anteriormente. Posteriormente definimos o tokenizador.
# aqui começamos a definir uma função de tokenização
def my_tokenizer(s):
# reduz as palavras para lowercase (letras minusculas)
s = s.lower()
# Faz a tokenização das palavras
tokens = nltk.tokenize.word_tokenize(s)
into words (tokens)
# remove palavras pequenas pois provavelmente não serão úteis
tokens = [t for t in tokens if len(t) > 2 ]
# remove as stopwords (palavras que não tem muito significado [The, where, was, etc]
tokens = [t for t in tokens if t not in stopwords]
# remove qualquer dígito (número)
tokens = t for t in tokens if not any (c.isdigit() for c in t)]
return tokens
Agora criaremos um mapa de indexação:
# Agora devemos criar um mapa word-to-index. Assim podemos criar os vetores de frequência mais tarde
# Vamos salvar também as versões tokenizadas (para não precisar tokenizar denovo)
word_index_map = {}
current_index = 0
all_tokens = []
all_titles = []
index_word_map = []
error_count = 0
for title in titles:
try:
title = title.encode('ascii', 'ignore').decode('utf-8') # Isso vai jogar uma exceção se tiverem caracteres errados
all_titles.append(title)
tokens = my_tokenizer(title)
all_tokens.append(tokens)
for token in tokens:
if token not in word_index_map:
word_index_map[token] = current_index
current_index += 1
index_word_map.append(token)
except Exception as e:
print(e)
print(title)
error_count += 1
## apenas exibe um exemplo
dict_items = word_index_map.items()
print("Exemplo do que cada vetor contém:n")
print("Word_index_map: ", list(dict_items)[:5])
print("title: ",all_titles[:1])
print("tokens: ", all_tokens[:1])
print("index_map: ", index_word_map[:1])
## mostra um relatório de erros
print("Number of errors parsing file:", error_count, "number of lines in file:", len(titles))
if error_count == len(titles):
print("There is no data to do anything with! Quitting...")
exit()
## saída
Exemplo do que cada vetor contém:
Word_index_map: [('philosophy', 0), ('sex', 1), ('love', 2), ('reader', 3), ('reading', 4)]
title: ['Philosophy of Sex and Love A Reader']
tokens: [['philosophy', 'sex', 'love', 'reader']]
index_map: ['philosophy']
Number of errors parsing file: 0 number of lines in file: 2373
Definimos algumas funções para tornar nossos tokens em um vetor:
# transforma tokens para vetores
def tokens_to_vector(tokens):
x = np.zeros(len(word_index_map))
for t in tokens:
i = word_index_map[t]
x[i] = 1
return x
Note que neste exemplo não temos nenhum rótulo. O PCA e o SVD são algoritmos não supervisionados, ou seja, eles aprendem a partir da estrutura dos dados e não para realizar predições.
a seguir nós criamos a matriz de dados
N = len(all_tokens)
D = len(word_index_map)
X = np.zeros((D, N)) # Cria uma matriz gigante de zeros baseado na quantidade de tokens e documentos
i = 0
#chama a função de transformação de vetores para cada linha do array
for tokens in all_tokens:
X[:,i] = tokens_to_vector(tokens)
i += 1
Note como nós divergimos da nossa matriz normal N x D e ao invés disso criamos D x N.
Finalmente, vamos usar o SVD para criar um scatterplot dos dados, ou seja reduzi-los a 2 dimensões e anotar cada ponto com sua palavra correspondente.
svd = TruncatedSVD()
Z = svd.fit_transform(X)
plt.scatter(Z[:,0], Z[:,1])
for i in range(D):
plt.annotate(s=index_word_map[i], xy=(Z[i,0], Z[i,1]))
plt.show()
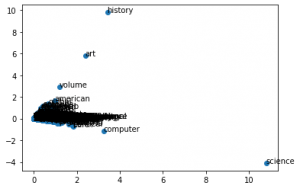
No Gráfico acima podemos perceber que ciências e história ficaram bastante separados, isso pode significar que essas palavras correlatas ficam agrupadas no mesmo vetor (ou seja, próximas).
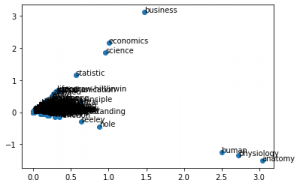
No gráfico acima fica masis evidente ainda que ciências (statistic, science, economics, business) estão mais próximos e destacados. Assim como human, physiology, anatomy (todas relacionadas entre sí).
Se você já usou o LSA, PCA ou SVD em outros conjuntos de dados, deixe seu comentário aqui e compartilhe com nossa comunidade.
