Nesse artigo vamos mostrar detalhadamente como funcionam as principais funções e portas lógicas. Vamos mostrar exemplos de circuitos e também como é a sua representação gráfica.
Antes de mais nada devemos distinguir Funções e Portas lógicas. As portas lógicas são portas que executam o processamento de duas ou mais entradas digitais (E, OU, NOT), enquanto as funções são mais complexas e são derivadas das portas lógicas básicas (NOU, XOU, etc).
Portas lógicas básicas
As portas lógicas são aquelas que executam a multiplicação lógica de duas ou mais entradas digitais, também chamadas variáveis booleanas, para então obtermos o valor de sua saída.
– E ou AND
A porta lógica E pode ser representada de acordo com a Figura 1:
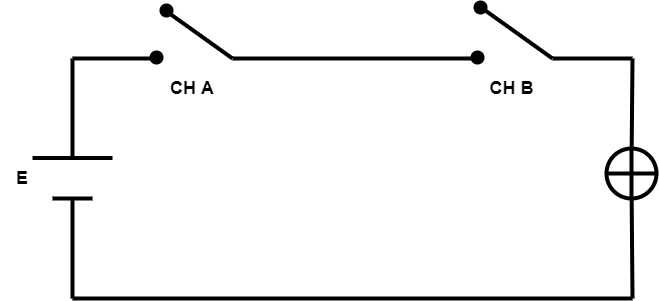
Esta lógica é bastante simples e somente se as duas “chaves” (CH A e CH B) estiverem com seu valor lógico ativo (1), que esta função será verdadeira. Utilizando a tabela da verdade para representação, esta função é representada da seguinte forma:
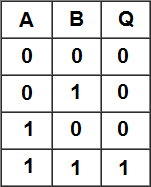
A expressão aritmética que representa esta porta lógica é: S = A . B
É importante notar que na porta lógica E, a saída será sempre 1 quando TODAS as variáveis forem 1. Graficamente a porta E é representada da seguinte forma:
 |
| Representação gráfica da porta E |
– OU ou OR
A porta lógica OU, também denominada OR pode ser representada a partir de um circuito, assim como o da Figura 2.
A lógica por trás desta porta é que se a porta CH A (Figura 2) ou a porta CH B estiverem fechadas, ou seja, na posição lógica igual a 1, a saída também será igual a 1. Acompanhe na tabela da verdade:
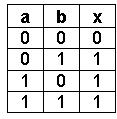
A expressão aritmética representante desta porta lógica é: S = A + B
Graficamente podemos representar a função OU da seguinte forma:
 |
| Representação gráfica da porta OU |
– NÃO ou NOT
A função lógica denominada NÃO ou NOT também denominado Inversor pode ser representado através do circuito da Figura 3.
| Figura 3 – circuito representativo da função NÃO |
Nesta função temos que sempre que a CH A estiver com o valor 1, a saída será seu inverso, portanto 0. O contrário também é verdadeiro. A tabela da verdade para esta função lógica é representada da seguinte forma:
| CH A | S |
| 1 | 0 |
| 0 | 1 |
A expressão aritmética que representa uma função inversora é: S = (A+B)’
Graficamente podemos representar a função NÃO da seguinte forma:
 |
| Representação gráfica da função NOT |
Derivadas
Estas funções têm este nome, pois são derivações das funções básicas. Ou seja, associações entre as funções básicas.
– NE, NÃO E ou NAND
Esta função representa uma negação, ou inversão da função E. Ou seja, consiste de uma associação entre a função E e a função NÃO. Esta função fica evidente quando observamos suas representações. Observe a Figura 4.
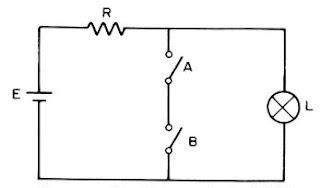 |
| Figura 4 – circuito representativo da função NÃO |
Esta função se comporta negando a função E. Assim, caso as entradas sejam ambas alimentadas com o valor lógico 1, a função negará e a saída será 0. Podemos observar este comportamento na tabela da verdade da função NE.
| A | B | S |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
A função NE também pode ser representada por sua expressão aritmética: S = A’.B’
Graficamente esta função pode ser representada da seguinte forma:

– NOU, NÃO OU ou NOR;
Assim como a função OU, esta função possui lógica semelhante. Porém, a inversora posicionada em conjunto faz a negação da função. A função NOU está representada na Figura 5.
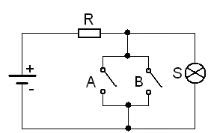 |
| Figura 5 – Circuito representativo da função NOU |
Como é possível observar no circuito caso a CH A ou a CH B sejam acionadas, a inversora fará efeito e a saída será 0. Caso isto não aconteça, a saída será 1. Acompanhe na tabela da verdade:
| A | B | S |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
A expressão aritmética que representa esta função: S = A’ + B’
A representação gráfica da função NOU pode ser feita da seguinte forma:
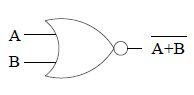 |
| Representação gráfica da função NOU |
– XOU, XOR ou OU exclusiva
A função Exclusive OU (XOU) supre uma necessidade ao qual as funções E ou OU combinadas não poderiam operar. Observe na Figura 6 o circuito representativo da função XOU.
O circuito representativo da função XOU mostra que SOMENTE se a entrada de A ou de B for 1, então a saída será 1. Caso ambas estejam em 0 ou em 1, a saída será 0. Para melhor entender essa função acompanhe a tabela da verdade:
| A | B | S |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
A expressão aritmética que representa esta estrutura é: S = A’. B + A . B‘
Graficamente podemos representar essa função da seguinte forma:
 |
| Representação gráfica da função XOU |
Todas as funções e portas lógicas estudadas nessa aula podem ser encontradas em vários programas de representação gráfica de circuitos digitais. Você poderá treinar sua construção e testar seu funcionamento simplesmente construindo o circuito digital.
Recomendo que vocês baixem o programa Logisim. Já usei muito ele e é excelente para estudantes dessa disciplina.