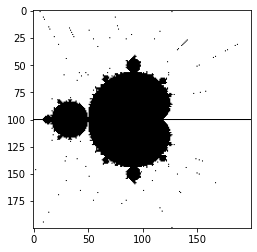
Nesse post vou mostrar pra vocês como é possível criar dois fractais muito legais usando a linguagem Python e algumas bibliotecas. Vamos criar passo a passo o fractal da árvore de Canopy e também conjunto de mendelbrot.
Se você gosta de fractais deveria visitar nosso post sobre o fractal de koch.
Preparação do ambiente
Antes de mais nada precisamos preparar nosso ambiente de desenvolvimento para construir nossos fractais. Lembre-se que alguns fractais podem até ser descritos como simples, porém exigem do programador uma certa destreza e conhecimento em alguns conceitos de estruturas de dados, recursão. Portanto, mesmo que para alguns isso seja trivial, sua construção pode ser bastante “difícil” de compreender.
Mas calma! eu vou te ajudar…
Árvores e recursão
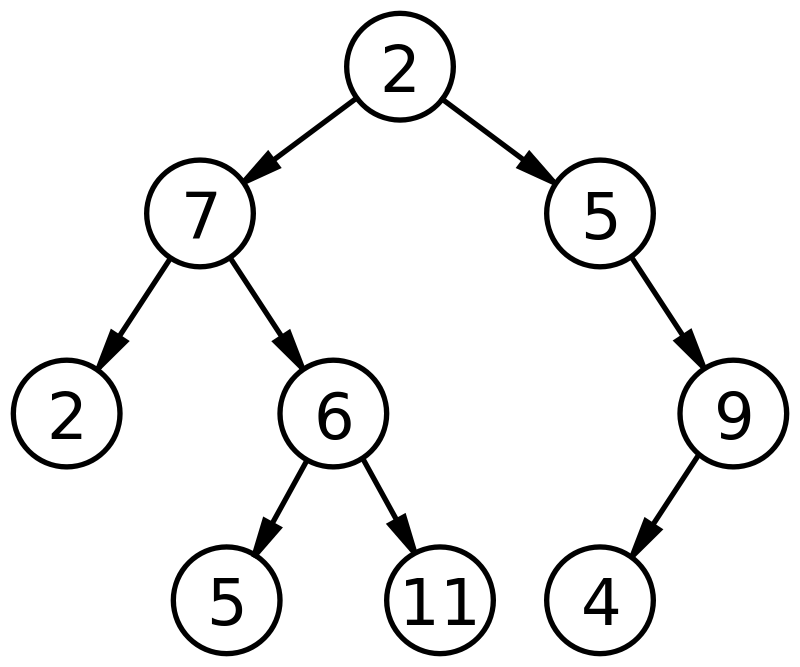
Primeiramente precisamos entender que vamos construir uma árvore, ou seja, vamos revisitar o tópico de árvores binárias. Em computação, uma árvore binária é uma estrutura que possui exatamente dois filhos para cada nó. Se essa árvore for de inteiros, teríamos algo mais ou menos assim:
As funções recursivas são definidas como “funções que chamam a sí mesma”. Claro que isso na prática pode gerar um loop infinito, sendo assim, uma função recursiva sempre tem um critério de parada. Um exemplo de uma estrutura básica de função recursiva seria:
def funcaoRecursiva(nivel, parada):
if nivel == parada:
return
else:
funcaoRecursiva(nivel + 1, parada)Se você já se lembrou do conceito árvore e também como usar recursões, isso já é o suficiente para reproduzir o fractal Canopy. Se não se lembra, vou deixar dois materiais interessantes:
Biblioteca Turtle
Certo, mas lembre-se que percorrer uma árvore é apenas uma parte do desafio, uma outra parte tem a ver com a biblioteca Turtle. Essa biblioteca faz referência a um tipo de gráfico chamados “gráficos de tartaruga” que usam um cursor relativo (a tartaruga) sobre o plano cartesiano para construir desenhos movimentando o eixo X e Y.
Na sua forma mais básica, a tartaruga tem três atributos: um local, uma orientação (ou direção) e uma caneta. Essa caneta, por sua vez também tem atributos: cor, largura e estado (ligado/desligado). Com esses comandos conseguimos controlar nossa tartaruga pela tela criando desenhos mais ou menos assim:

Mas não se engane, esse tipo de desenho pode se tornar muito complexo e legais, veja alguns exemplos:

Se você quer criar programas usando essa biblioteca basta você digitar:
# para importar nossa "tartaruga" fazemos:
import turtle
# mover a tartaruga para frente:
turtle.forward(100)
# finalizar o processamento
turtle.done()Os comandos básicos de movimentação são:
# para importar nossa "tartaruga" fazemos:
import turtle
# mover a tartaruga para frente:
turtle.forward(100)
turtle.right(90)
turtle.forward(100)
turtle.right(90)
turtle.forward(100)
turtle.right(90)
turtle.forward(100)
turtle.right(90)
# finalizar o processamento
turtle.done()Algo importante que venho percebendo dentro do Windows e também do Mac é que essa biblioteca ao finalizar a visualização pode forçar a interrupção do kernel. Aparentemente o programa entre em loop infinito e o sistema operacional obriga sua interrupção. Então para mitigar isso adicionei dos comandos extras:
# para importar nossa "tartaruga" fazemos:
import turtle
# pega as propriedades da tela
wn = turtle.Screen()
# mover a tartaruga para frente:
turtle.forward(100)
turtle.right(90)
turtle.forward(100)
turtle.right(90)
turtle.forward(100)
turtle.right(90)
turtle.forward(100)
turtle.right(90)
# finaliza ao clicar
wn.exitonclick()
# finalizar o processamento
turtle.done()Maravilha, com esses comandos já conseguimos começar a criar nossa árvore canopy.
Árvore Canopy
Esse é considerado o fractal mais simples de todos e é composto apenas por linhas retas que vão se bifurcando até formar algo que se parece com uma árvore, algo mais ou menos assim:

Quando queremos percorrer uma árvore assim, é preciso usar nossa velha amiga recursão. Mas antes, vamos preparar todo nosso ambiente usando a biblioteca:
# para importar nossa "tartaruga" fazemos:
import turtle
# define nossa tartaruga
t = turtle.Turtle()
# "pega" a nossa tela
wn = turtle.Screen()
# define a profundidade desejada na recursão
profundidade = 3
# coloca o angulo inicial para cima para cima
t.right(270)
#coloca a tartaruga na posição inicial
t.penup()
t.goto((0,-250))
t.pendown()
# modifica a velocidade (para ir mais rápido)
t.speed(150)
# aqui ficará nosso código
# finalizar o processamento
wn.exitonclick()
turtle.done()Certo, depois de preparado, podemos inserir um pouco de código recursivo simplesmente para desenhar um risco reto (que seria o tronco da nossa árvore):
# para importar nossa "tartaruga" fazemos:
import turtle
# define nossa tartaruga
t = turtle.Turtle()
# "pega" a nossa tela
wn = turtle.Screen()
# define a profundidade desejada na recursão
profundidade = 3
# coloca o angulo inicial para cima para cima
t.right(270)
#coloca a tartaruga na posição inicial
t.penup()
t.goto((0,-250))
t.pendown()
# modifica a velocidade (para ir mais rápido)
t.speed(150)
# define a função recursiva:
# i → representa o tamanho do segmento
# p → representa a profundidade desejada
# mP → representa a profundidade atual
def canopy(i, p, mP):
if p == mP:
return
else:
t.forward(i)
canopy(100, profundidade, 0)
# finalizar o processamento
wn.exitonclick()
turtle.done()O resultado fica assim:
Agora que já temos o nosso primeiro tronco, podemos fazer um comando para virar 30º e mover para frente:
# para importar nossa "tartaruga" fazemos:
import turtle
# define nossa tartaruga
t = turtle.Turtle()
# "pega" a nossa tela
wn = turtle.Screen()
# define a profundidade desejada na recursão
profundidade = 3
# coloca o angulo inicial para cima para cima
t.right(270)
#coloca a tartaruga na posição inicial
t.penup()
t.goto((0,-250))
t.pendown()
# modifica a velocidade (para ir mais rápido)
t.speed(150)
# define a função recursiva:
# i → representa o tamanho do segmento
# p → representa a profundidade desejada
# mP → representa a profundidade atual
def canopy(i, p, mP):
if p == mP:
return
else:
t.forward(i)
t.left(30)
t.forward(i)
canopy(100, profundidade, 0)
# finalizar o processamento
wn.exitonclick()
turtle.done()O resultado fica assim:
Ficou ótimo, mas ainda não está nem parecido com uma árvore. Isso porquê não estou desenhando nada usando a recursão como aliada. Então agora o que vou fazer é simplesmente adicionar uma chamada recursiva que a cada nível reduz nossa linha em 25% e entorta ela em 30º.
# para importar nossa "tartaruga" fazemos:
import turtle
# define nossa tartaruga
t = turtle.Turtle()
# "pega" a nossa tela
wn = turtle.Screen()
# define a profundidade desejada na recursão
profundidade = 5
# coloca o angulo inicial para cima para cima
t.right(270)
#coloca a tartaruga na posição inicial
t.penup()
t.goto((0,-250))
t.pendown()
# modifica a velocidade (para ir mais rápido)
t.speed(150)
tamanhoDoSegmento = 200
# define a função recursiva:
def canopy(i, p, mP):
if p == mP:
return
else:
t.forward(i)
t.left(30)
canopy(0.75*i, p, mP + 1)
canopy(100, profundidade, 0)
# finalizar o processamento
wn.exitonclick()
turtle.done()O resultado fica assim:
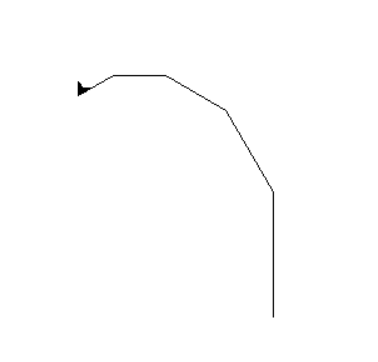
Agora temos algo que parece com um galho, porém, precisamos do restante da árvore! vamos desenhar então galhos da esquerda e da direita:
# para importar nossa "tartaruga" fazemos:
import turtle
# define nossa tartaruga
t = turtle.Turtle()
# "pega" a nossa tela
wn = turtle.Screen()
# define a profundidade desejada na recursão
profundidade = 5
# coloca o angulo inicial para cima para cima
t.right(270)
#coloca a tartaruga na posição inicial
t.penup()
t.goto((0,-250))
t.pendown()
# modifica a velocidade (para ir mais rápido)
t.speed(150)
tamanhoDoSegmento = 200
# define a função recursiva:
def canopy(i, p, mP):
if p == mP:
return
else:
t.forward(i)
t.left(30)
canopy(0.75*i, p, mP + 1)
t.right(60)
canopy(0.75*i, p, mP + 1)
canopy(100, profundidade, 0)
# finalizar o processamento
wn.exitonclick()
turtle.done()O resultado disso é algo assim:
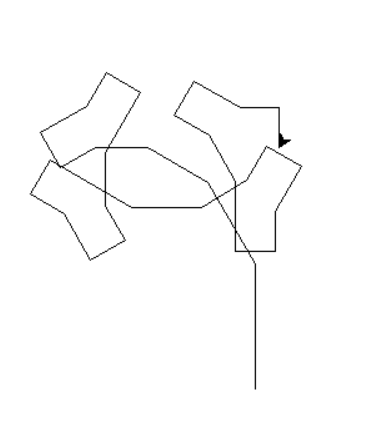
Claramente algo deu errado né?
Isso aconteceu porque nós não adicionamos um comando de “volta” para nossa tartaruga. Então ao adicionar esse comando:
# para importar nossa "tartaruga" fazemos:
import turtle
# define nossa tartaruga
t = turtle.Turtle()
# "pega" a nossa tela
wn = turtle.Screen()
# define a profundidade desejada na recursão
profundidade = 5
# coloca o angulo inicial para cima para cima
t.right(270)
#coloca a tartaruga na posição inicial
t.penup()
t.goto((0,-250))
t.pendown()
# modifica a velocidade (para ir mais rápido)
t.speed(150)
tamanhoDoSegmento = 200
# define a função recursiva:
def canopy(i, p, mP):
if p == mP:
return
else:
t.forward(i)
t.left(30)
canopy(0.75*i, p, mP + 1)
t.right(60)
canopy(0.75*i, p, mP + 1)
t.left(30)
t.backward(i)
canopy(100, profundidade, 0)
# finalizar o processamento
wn.exitonclick()
turtle.done()Finalmente o resultado é esse:
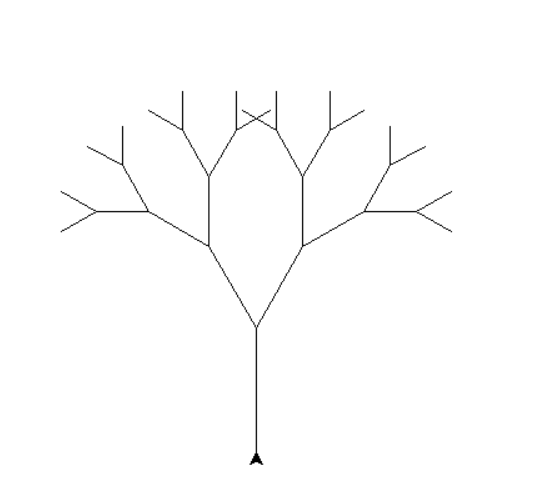
No código alternativo disponível em nosso github, você vê uma foma diferente de construir a árvore (com angulações diferentes).
# para importar nossa "tartaruga" fazemos:
import turtle
t = turtle.Turtle()
wn = turtle.Screen()
depth = 7
myDepth = 0
branchSize = 100
turtle.screensize(canvwidth=500, canvheight=500,
bg="white")
# mover a tartaruga para frente:
t.penup()
t.goto(x = (0, -200))
t.pendown()
t.forward(100)
t.back(200)
t.forward(100)
t.left(90)
def drawSegment(myDepth, depth, rightt):
if myDepth >= depth:
return 0
else:
t.forward(branchSize * (0.8 ** myDepth))
t.left(45 * (0.6 ** myDepth))
drawSegment(myDepth+1, depth, 0)
t.right(90 * (0.6 ** myDepth))
drawSegment(myDepth + 1, depth , 1)
t.left(45 * (0.6 ** myDepth))
t.back(branchSize * (0.8 ** myDepth))
# finalizar o processamento
drawSegment(myDepth, depth, 0)
wn.exitonclick()
turtle.done()O resultado disso é:
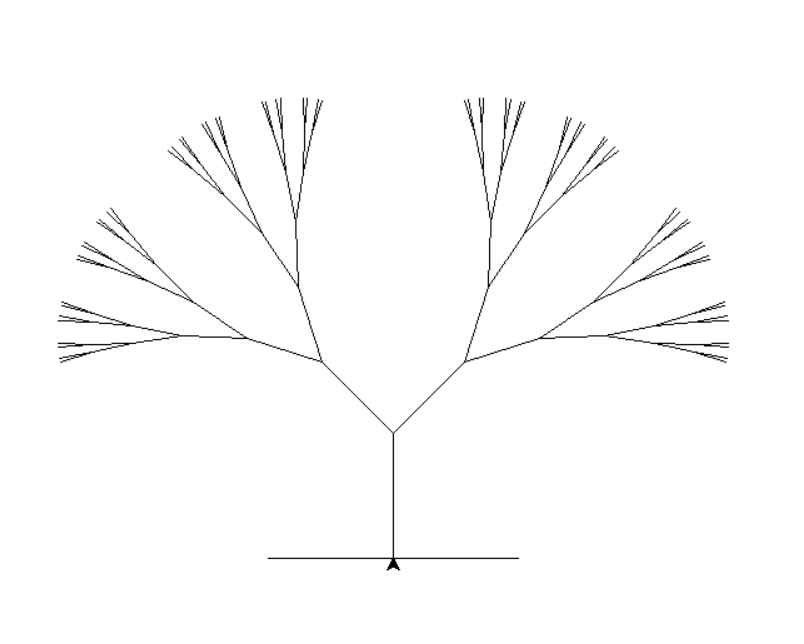
Fractal de Mendelbrot
Esse fractal é um dos mais famosos que existem e ela transcendeu apenas o mundo da matemática, sendo ele estudado em vários campos (inclusive na computação). Esse fractal foi definido pela primeira vez pelos matemáticos franceses Pierre Fatou e Gaston Julia no início do século XX. Ele só foi desenhado pela primeira vez em 1978 por Robert W. Brooks e Peter Matelski em um grupo de estudos Kleilianos.
Essa foi a primeira foto publicada desse fractal:
O fractal é desenhado baseando-se em um conjunto de números complexos. Mas o que seria isso?
Bom, basicamente números complexos são:
Em matemática , um número complexo é um elemento de um sistema numérico que contém os números reais e um elemento específico denotado i , chamado de unidade imaginária , e que satisfaz a equação i² = −1 . Além disso, todo número complexo pode ser expresso na forma a + bi , onde a e b são números reais. Porque há números reais satisfaz a equação acima, i foi chamado um número imaginário por René Descartes .
Fonte: Wikipedia
Para mostrar nosso fractal precisamos entender que a imagem é composta por dois eixos, sendo um deles imaginário e o outro real (isso é chamado de plano complexo).
Então seria algo assim:
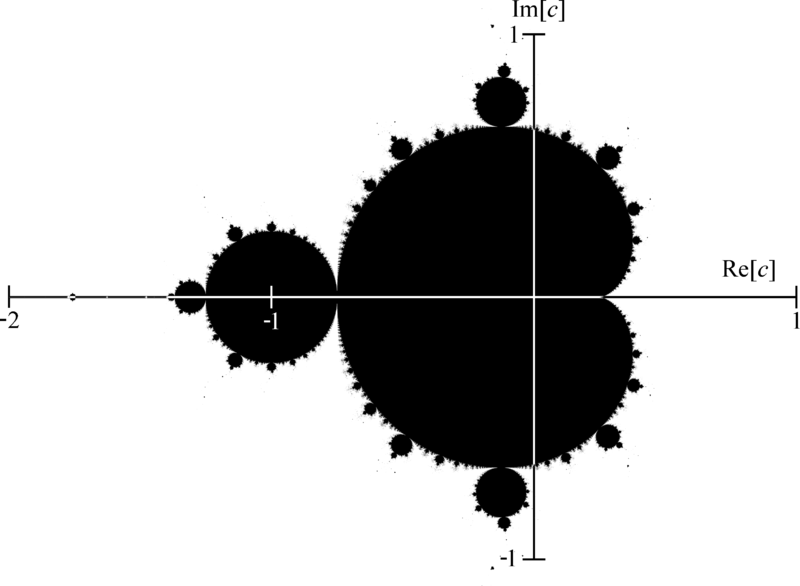
Veja que esse conjunto está posicionado no eixo real entre -2 e 1 e para o eixo imaginário entre 1 e -1 (isso vai ser importante).
Então para mostrarmos essa imagem usando nosso amigo Python precisamos mapear um conjunto de pixels (imagem) entre esses dois valores. Por exemplo: se minha imagem possui 200 por 200, então no eixo X eu preciso mapear cada pixel para corresponder a um número no intervalo de -2 e 1.
Essa função pode ser definida como:
## função auxiliar:
def translate(value, leftMin, leftMax, rightMin, rightMax):
# Figure out how 'wide' each range is
leftSpan = leftMax - leftMin
rightSpan = rightMax - rightMin
# Convert the left range into a 0-1 range (float)
valueScaled = float(value - leftMin) / float(leftSpan)
# Convert the 0-1 range into a value in the right range.
return rightMin + (valueScaled * rightSpan)Essa função pega 5 parâmetros:
- Value: representa o valor que queremos fazer a transposição
- leftMin: representa o mínimo que podemos atingir (no plano da imagem) – nesse caso seria zero
- leftMax: representa o máximo que podemos atingir no plano da imagem – nesse caso seria 200
- rightMin: seria o mínimo que queremos na transposição (ex. -2)
- rightMax: seria o máximo que queremos na transposição (ex. 1)
Bom, agora, seria uma boa hora para explicar a parte matemática… mas eu confesso que não seria uma explicação muito boa, então vou deixar o Daniel Shiffman explicar:
Antes de mais nada, se você gosta de entender sobre como as máquinas podem gerar “obras de arte”, não esqueça de ver o podcast Hipsters.tech que fala sobre arte generativa.
Certo, se você viu o vídeo completo, deve ter percebido que ele usou o P5.js para criar o fractal. Nós vamos usar o Python, então preciso fazer exatamente o que ele fez porém usando nossas bibliotecas gráficas e tudo mais. Então vou primeiro lembrar você que estou usando essa função para mostrar imagens:
import re
import numpy as np
from matplotlib import pyplot as plt
## mostra sem salvar em um arquivo
def mostrarImagem(mapa, save = False, path = "", animation = False, index = 0, direction = ""):
ni = np.array(mapa)
plt.imshow(ni, cmap='gray')
if save == False:
plt.show()
if save == True and animation == False:
plt.savefig(pathToSave.format("output.png"))
if save == True and animation == True:
plt.savefig(pathToSave.format(str(index) + "Fig" + direction + ".png"))Essa função só requer 1 parâmetro que é um mapa de pixels em forma de função, portanto, facilmente você consegue uma imagem assim:
mp = [10,10,10,10,10,10,10,10,10,10,10,10] mp2 = [0,0,0,0,0,0,0,0,0,0,0,0] mp3 = [5,5,5,5,5,5,5,5,5,5,5,5] mapa = [] mapa.append(mp) mapa.append(mp2) mapa.append(mp3) mapa.append(mp2) mapa.append(mp) mapa.append(mp3) mapa.append(mp2) mostrarImagem(mapa)

Para escrever um simples ponto eu uso uma função:
import numpy as np
def escrevePonto(imagem,x,y,pontosDeCinza):
img = np.array(imagem)
img[y,x] = pontosDeCinza
return img
imagem = escrevePonto(imagem,6,5,15)
mostrarImagem(imagem)Certo, antes de mais nada, vamos criar uma nova imagem:
imagem = criarImagem(200,200,15)
imagem = escrevePonto(imagem,50,50,15)
mostrarImagem(imagem)Agora podemos criar nosso plano complexo:
## vamos definir aqui um valor de width e height
width = 200
height = 200
imagem = criarImagem(width,height,15)
maxiterations = 100;
for x in range (width):
for y in range(height):
## o código vai aqui
mostrarImagem(imagem)Bom, precisamos fazer o translate dos pontos usando nossa função:
## vamos definir aqui um valor de width e height
width = 200
height = 200
imagem = criarImagem(width,height,15)
maxiterations = 100;
for x in range (width):
for y in range(height):
#print(y/50*100, "%")
a = translate(x,0, width,-1.5,1.5)
b = translate(y,0, height,-1.5,1.5)
mostrarImagem(imagem)
Esses valores serão usados na nossa próxima tarefa que é fazer os cálculos com números complexos:
## vamos definir aqui um valor de width e height
width = 200
height = 200
imagem = criarImagem(width,height,15)
maxiterations = 100;
for x in range (width):
for y in range(height):
#print(y/50*100, "%")
a = translate(x,0, width,-1.5,1.5)
b = translate(y,0, height,-1.5,1.5)
ca = a
cb = b
n = 0
while (n < maxiterations):
# calculo com números complexos
aa = a* a -b * b
bb = 2* a * b
a = aa + ca
b = bb + cb
# aqui verificamos se o número tende ao infinito
if (a * (a + b) * b > 16):
break
n += 1
bright = 15
# aqui se o numero tende ao infinito ele escreve "0" (preto)
# se o número não tende ao infinito ele escreve "15" (branco)
# tudo que está dentro do conjunto tende ao infinito
if n == maxiterations:
bright = 0
imagem = escrevePonto(imagem,x,y,bright)
mostrarImagem(imagem)